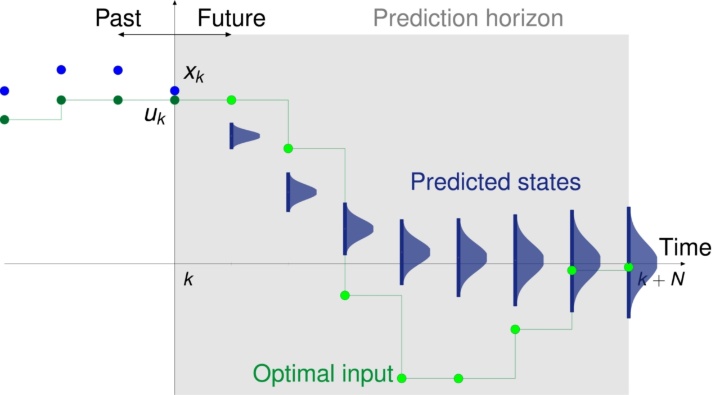
Model predictive control (MPC), also referred to as moving horizon control or receding horizon control, is one of the most successful and most popular advanced control methods. The basic idea of MPC is to predict the future behavior of the controlled system over a finite time horizon and compute an optimal control input that, while ensuring satisfaction of given system constraints, minimizes an a priori defined cost functional. To be more precise, the control input is calculated by solving at each sampling instant a finite horizon open-loop optimal control problem; the first part of the resulting optimal input trajectory is then applied to the system until the next sampling instant, at which the horizon is shifted and the whole procedure is repeated again. MPC is in particular successful due to its ability to explicitly incorporate hard state and input constraints as well as a suitable performance criterion into the controller design.
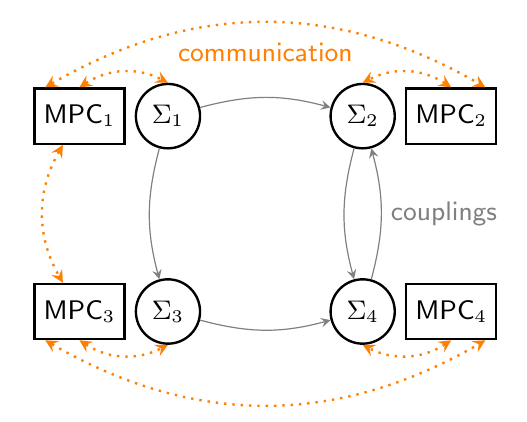 In large-scale dynamical systems and networks of cooperating systems, it is often impossible or undesirable to control the overall system with one centralized controller. Hence, in recent years, the field of distributed MPC has gained significant attention, where each of the subsystems ∑i is locally controlled by an MPC controller and exchanges information about predicted trajectories with its neighbors, in order to ensure satisfaction of coupling constraints and achievement of the overall control objective. At the IST, distributed MPC schemes are developed which besides the classical goal of setpoint stabilization are also suited for more general cooperative control tasks, including for example consensus and synchronization problems, or optimal operation with respect to some real "economic" costs.
In large-scale dynamical systems and networks of cooperating systems, it is often impossible or undesirable to control the overall system with one centralized controller. Hence, in recent years, the field of distributed MPC has gained significant attention, where each of the subsystems ∑i is locally controlled by an MPC controller and exchanges information about predicted trajectories with its neighbors, in order to ensure satisfaction of coupling constraints and achievement of the overall control objective. At the IST, distributed MPC schemes are developed which besides the classical goal of setpoint stabilization are also suited for more general cooperative control tasks, including for example consensus and synchronization problems, or optimal operation with respect to some real "economic" costs.
Contact Persons: Frank Allgöwer, Matthias Köhler
Publications:
- M. Köhler, M. A. Müller, and F. Allgöwer.
Data-driven distributed MPC of dynamically decoupled linear systems
In Proc. 25th Int. Symp. Mathematical Theory of Networks and Systems (MTNS), Bayreuth, Germany, 2022, pp. 365–370. doi: 10.1016/j.ifacol.2022.11.080 - M. Hirche, P. N. Köhler, M. A. Müller, and F. Allgöwer.
Distributed Model Predictive Control for Consensus of Constrained Heterogeneous Linear Systems.
In Proc. of the 59th IEEE Conf. on Decision and Control (CDC), Jeju Island, Republic of Korea, 2020, pp. 1248–1253. doi: 10.1109/CDC42340.2020.9303838 - P. N. Köhler, M. A. Müller, and F. Allgöwer.
Graph topology and subsystem centrality in approximately dissipative system interconnections.
In Proc. of the 58th IEEE Conference on Decision and Control, Nice, France, 2019, pp.787-792. - P. N. Köhler, M. A. Müller, and F. Allgöwer.
Approximate dissipativity and performance bounds for interconnected systems.
In Proc. of the European Control Conference, Naples, Italy, 2019, pp.787-792. [preprint] - P. N. Köhler, M. A. Müller, and F. Allgöwer.
A distributed economic MPC framework for cooperative control under conflicting objectives.
Automatica, vol. 96, pp. 368-379, 2018. - M. A. Müller, and F. Allgöwer.
Economic and distributed model predictive control: recent developments in optimization-based control.
SICE Journal of Control, Measurement, and System Integration, vol. 10, no. 2, pp.39-52, March 2017. - M. A. Müller, M. Reble, and F. Allgöwer.
Cooperative control of dynamically decoupled systems via distributed model predictive control.
International Journal of Robust and Nonlinear Control, vol. 22, no. 12, pp. 1376-1397, 2012.
In Robust MPC, the goal is to stabilize uncertain systems or systems that are affected by disturbances while ensuring robust satisfaction of constraints. The behavior of such systems cannot be predicted exactly. If bounds on the uncertainty are known, however, it is possible to determine bounds on the future system behavior. Feasibility and stability can be established using set-theoretic methods.
The drawback of many existing robust MPC schemes is a high computational load due to the complexity involved in set-valued predictions as well as conservatism induced by these methods. In order to provide a computationally efficient formulation for nonlinear systems, we propagate the uncertainty along the predicted trajectory online using computed bounds based on incremental system properties. Robustness is then achieved by using a suitable constraint tightening based on the predicted bound on the uncertainty. We show how this approach can also be extended for the case of robust obstacle avoidance with moving obstacles.
We are also using robust MPC methods to design fast and safe approximate explicit MPC in combination with offline function approximation methods from machine learning.
In many practical applications, where the available computational power might be significantly reduced, online robust MPC approaches cannot be employed. We propose an offline approach, able to deal with general uncertainty, i.e. state and input dependent, which constructs tightened constraint sets offline, and therefore keeps the computational load unchanged with respect to a nominal MPC.
The set-theoretic methods of robust MPC can also be extended to scenarios where the main goal is not the stabilization of a set-point but to operate the system optimally with respect to some economic criterion like energy consumption. We propose a robust economic MPC algorithm, which explicitly considers the possible disturbances within the optimization problem instead of optimizing the nominal behavior, and we are able to provide bounds on the average and worst-case performance and thus robustness of the economic objective.
Contact Persons: Frank Allgöwer, Lukas Schwenkel
Publications:
- L. Schwenkel, J. Köhler, M. A. Müller, F. Allgöwer
Model predictive control for linear uncertain systems using integral quadratic constraints
Transactions of Automatic Control (TAC), 2023, vol. 68, no. 1, pp. 355-368. - J. Köhler, R. Soloperto, M. A. Müller, F. Allgöwer
A computationally efficient robust model predictive control framework for uncertain nonlinear systems
Transactions of Automatic Control (TAC), 2021, vol. 66, no. 2, pp. 794-801. - F. D. Brunner, M. A. Müller and F. Allgöwer.
Enhancing Output-feedback mpc with Set-valued Moving Horizon Estimation
IEEE Transactions on Automatic Control, 63.9 (2018): 2976-2986. - R. Soloperto, J. Köhler, M. A. Müller, F. Allgöwer
Collision avoidance for uncertain nonlinear systems and moving obstacles using robust Model Predictive Control
European Control Conference (ECC), 2019 - F. A. Bayer, M. A. Müller, F. Allgöwer
On optimal system operation in robust economic MPC
Automatica, 2018, Volume 88, pp. 98-106
Cooperations
- Matthias A. Müller, Leibniz University Hannover, Germany
In Stochastic Model Predictive Control, uncertainty in the system description or external disturbances are taken explicitely into account in the design process. In contrast to Robust MPC, where uncertainties are usually assumed to be unknown but bounded and constraints should be satisfied for all possible realizations, this approach assumes stochastic disturbance or parameter variations. This assumption allows to design controllers which optimize the expected value or other risk measures rather than the worst case. Performance can be further increased by allowing an a priori specified probability of constraint violation. The focus of our research in Stochastic MPC are computationally tractable formulations of the constraints and objective as well as ensuring recursive feasibility. To this end deterministic and sample based methods are taken into account.
Contact Persons: Frank Allgöwer, Henning Schlüter
Publications:
- Schlüter, H. and Allgöwer, F.
A Constraint-Tightening Approach to Nonlinear Stochastic Model Predictive Control under General Bounded Disturbances
Proc. 21th IFAC World Congress, 2020. - Schlüter, H. and Allgöwer, F.
Stochastic model predictive control using initial state optimization
Proc. 25th Int. Symp. Math. Theory of Networks and Systems (MTNS), 2022.
The most well-studied MPC approaches with guaranteed stability consider the problem of stabilizing a given steady-state and use an offline designed control Lyapunov function as a terminal cost. However, in practical applications the control goal is often more general, involving dynamic operation, such as setpoint tracking, trajectory tracking, path following, output regulation or general economic optimal control (e.g. minimizing energy consumption or maximizing production). Furthermore, the optimal mode of operation (e.g. optimal periodic orbit or steady-state) is often subject to online changes, e.g. due to externally set references or changing price signals. Finally, the usage of a suitable terminal cost is limited in many practical applications due to the intractability of the offline design for this challenging setup.
At the IST, we aim at bridging this gap between existing theoretical approaches and practical challenges by providing suitable analysis and design tools. We study the theoretical properties of simple tracking MPC schemes without a terminal cost using incremental system properties. Furthermore, we develop reference generic offline computations that can be used to obtain a suitable terminal cost for dynamic operation of nonlinear systems. Finally, we design MPC schemes that can operate reliably under online changing dynamic target signals, by combining the reference generic offline computation with artificial reference trajectories/setpoints.
Contact Persons: Frank Allgöwer, Matthias Köhler, Lukas Schwenkel
Publications:
- L. Schwenkel, A. Hadorn, M. A. Müller, F. Allgöwer
Linearly discounted economic MPC without terminal conditions for periodic optimal operation
Automatica, vol. 156, pp. 111393, 2024 - M. Köhler, M. A. Müller, F. Allgöwer
Transient Performance of MPC for Tracking
IEEE Control Systems Letters, 7, 2545-2550, 2023 - J. Köhler, M. A. Müller, F. Allgöwer
Nonlinear reference tracking: An economic model predictive control perspective
Transactions of Automatic Control (TAC), 64.1 (2018): 254-269. - J. Köhler, M. A. Müller, F. Allgöwer
A nonlinear model predictive control framework using reference generic terminal ingredients
Transactions of Automatic Control (TAC). - J. Köhler, M. A. Müller, F. Allgöwer
A nonlinear tracking model predictive control scheme for dynamic target signals
Automatica. - J. Köhler, M. A. Müller, F. Allgöwer
Periodic optimal control of nonlinear constrained systems using economic model predictive control
Journal of Process Control, submitted.
Cooperations
- Matthias A. Müller, Leibniz University Hannover, Germany
Robust and Stochastic MPC methods are based on the construction of forward reachable sets that take into account some, or all, of the possible realization of the uncertainty. Despite these approaches provide theoretical guarantees, are often too conservative due to the over-approximation of the uncertainty in the system. In order to get a better estimate of the system, and therefore to reduce the uncertainty, well-known techniques in system identification can be employed.
Adaptive MPC combines approaches taken from Robust and Stochastic MPC, with learning techniques, in order to obtain an improvement in performances with a constantly updated system, while guaranteeing formal properties. It is important to note that in this case the MPC controller is decoupled from the chosen learning technique, and therefore it behaves in a so-called Certainty Equivalence fashion (CE- MPC).
In contrast to Adaptive MPC, where the system is learned as a side effect of the control action, in Learning MPC (also called dual-adaptive MPC) we explicitly include in the MPC optimization problem ways to improve performances. Providing formal guarantees such as stability and constraint satisfaction is considered as one open point, and is the focal point of our research.
In the literature, the main approaches in Learning MPC can be subdivided into three main categories:
- Learning the system;
- Learning the terminal cost;
- Learning safe sets.
Performance and results might differ significantly based on the chosen approach.
Contact Persons: Frank Allgöwer
Publications:
- R. Soloperto, J. Köhler, M. A. Müller, F. Allgöwer
Dual Adaptive MPC for output tracking of linear systems
58th Conference on Decision and Control - M. Hertneck, J. Köhler, S. Trimpe , F. Allgöwer
Learning an approximate Model Predictive Controller with Guarantees
IEEE Control Systems Letters, 2.3 (2018): 543-548. - R. Soloperto, M. A. Müller, S. Trimpe, F. Allgöwer
Learning-Based Robust Model Predictive Control with State-Dependent Uncertainty
6th IFAC Conference on Nonlinear Model Predictive Control
Cooperations
- Matthias A. Müller, Leibniz University Hannover, Germany
- Sebastian Trimpe, Max Planck Institute for Intelligent Systems (MPI-IS), Stuttgart, Germany
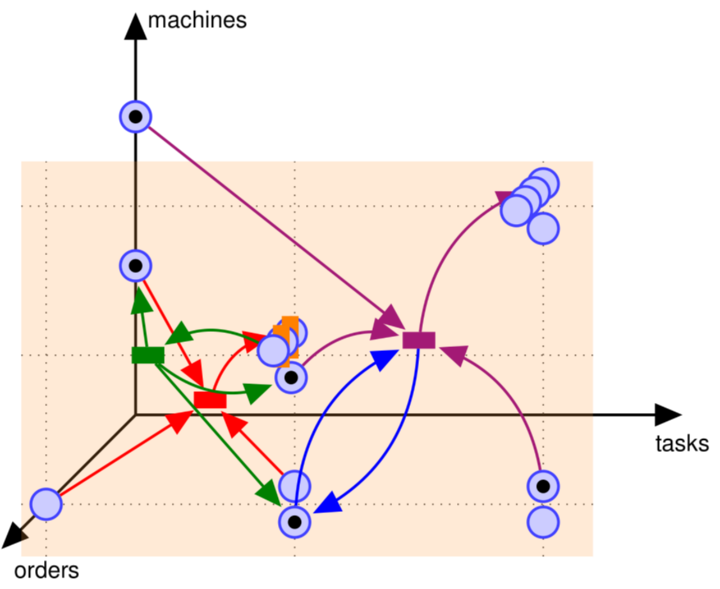
Industry 4.0 refers to the fundamental changes in the industrial production that are expected in the next years. The term Industry 4.0 is not defined precisely and comprises various enabling technologies and desired goals, which require research in diverse scientific disciplines. Therefore, the research on Industry 4.0 conducted at the IST is interdisciplinary and brings its strengths in systems and control theory to the developments in operations research, factory planning and management.
At the IST, methods from MPC are examined with respect to their suitability for the control of the factories of the future. While MPC has most of its industrial applications in process industry, production and assembly systems are only considered rarely. Since these systems comprise a great part of the changing industrial environment, novel MPC schemes are developed for the scheduling and dynamic rescheduling of production and assembly systems. Based on a novel modeling framework which makes these systems accessible for the development and the systems theoretic analysis of MPC schemes, closed loop guarantees for the desired system properties are given.
Contact Persons: Frank Allgöwer
Publications:
- K. D. Listmann, P. Wenzelburger and F. Allgöwer.
Industrie 4.0 - (R)evolution without Control Technologies?
Journal of The Society of Instrument and Control Engineers, pp.555-565, 2016. - P. Wenzelburger and F. Allgöwer.
A Petri Net Modeling Framework for the Control of Flexible Manufacturing Systems.
In Proc. of the 9th IFAC Conference on Manufacturing Modelling, Management and Control, pp. 522-528, 2019. - P. Wenzelburger and F. Allgöwer.
A Novel Optimal Online Scheduling Scheme for Flexible Manufacturing Systems.
In Proc. of the 13th IFAC Workshop on Intelligent Manufacturing Systems, pp.1-6, 2019
Research pages regarding MPC for networked systems and data-driven control can be found here: Networked systems , Data driven control